2018/10/26 ACM集训第二次周赛题解及自身题目优化
问题A:海港
题目描述:
输入:
输出:
输出n行,第i行输出一个整数表示第i艘船到达后的统计信息。
样例输入
3
1 4 4 1 2 2
2 2 2 3
10 1 3
样例输出
3
4
4
提示
【样例解释1】
第一艘船在第1秒到达海港,最近24小时到达的船是第一艘船,共有4个乘客, 分别是来自国家4,1,2,2共来自3个不同的国家;
第二艘船在第2秒到达海港,最近24小时到达的船是第一艘船和第二艘船,共有4 + 2 =6个乘客,分别是来自国家4,1,2,2,2,3共来自4个不同的国家;
第三艘船在第10秒到达海港,最近24小时到达的船是第一艘船、第二艘船和第 三艘船,共有4+ 2+1=7个乘客,分别是来自国家4,1,2,2,2,3,3共来自4个不同 的国家。
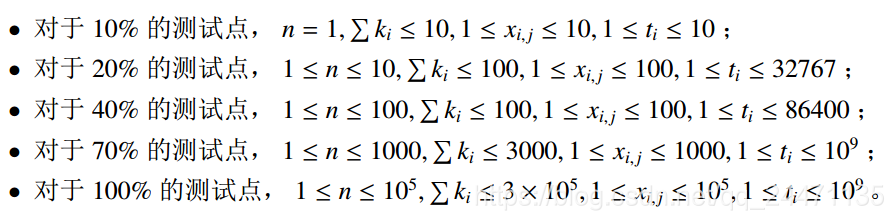
分析:对于这个题一开始想用二维数组,但是编译崩溃,所以就没有做出来,基础知识还是不足,后来通过题解,了解到了结构体,并思考可以使用两个一维数组来实现。这个题的思路在于记录时间和船上人员的国籍,时间用来保证所记录的是24小时之内的船只,而国籍则可以利用桶来找出国籍的数量。
#include<bits/stdc++.h>
using namespace std;
struct people
{
int time,ct;
}a[300005];
int main()
{
int n,i,cont=0;
int b[100005]={0};
scanf("%d",&n);
int head=0;
int k=0;
for(i=1;i<=n;i++)
{
int Time,Peo,t;
scanf("%d%d",&Time,&Peo);
for(t=0;t<Peo;t++)
{
scanf("%d",&a[k].ct);
a[k].time=Time;
if(b[a[k].ct]==0) cont++;
b[a[k].ct]++;
k++;
}
while(Time-a[head].time>=86400)
{
b[a[head].ct]--;
if(b[a[head].ct]==0) cont--;
head++;
}
printf("%d\n",cont);
}
return 0;
}```
**问题B:魔法阵(待解决)**
**问题C:金币**
题目描述
国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天 (第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚 金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式 会一直这样延续下去:当连续 N 天每天收到 N 枚金币后,骑士会在之后的连续 N+1 天 里,每天收到 N+1 枚金币。 请计算在前 K 天里,骑士一共获得了多少金币。
输入
输入文件只有 1 行,包含一个正整数 K,表示发放金币的天数。
输出
输出文件只有 1 行,包含一个正整数,即骑士收到的金币数。
样例输入
6
样例输出
14
提示
【输入输出样例 说明】
骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天, 每天收到三枚金币。因此一共收到 1+2+2+3+3+3=14 枚金币。
【数据说明】 对于 100%的数据,1 ≤ K ≤ 10,000。
分析:这是一个简单的循环体题目,给金币天数与金币数相同,且逐渐增长。
```c
#include<bits/stdc++.h>
using namespace std;
int main()
{
int sum=0,i=1,k=1,day=0,DAY;
scanf("%d",&DAY);
while(day<DAY)
{
for(i=1;i<=k;i++)
{
sum+=k;
day++;
if(day==DAY)
break;
}
k++;
}
printf("%d",sum);
}
问题D:回文日期
题目描述
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用8位数字表示一个日期,其中,前4位代表年份,接下来2位代表月 份,最后2位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表 示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的8位数字是回文的。现 在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存 在的日期是回文的。
一个8位数字是回文的,当且仅当对于所有的i(1<= i <= 8)从左向右数的第i个 数字和第9-i个数字(即从右向左数的第i个数字)是相同的。
例如:
•对于2016年11月19日,用8位数字20161119表示,它不是回文的。
•对于2010年1月2日,用8位数字20100102表示,它是回文的。
•对于2010年10月2日,用8位数字20101002表示,它不是回文的。
每一年中都有1212个月份:
其中,1,3,5,7,8,10,121,3,5,7,8,10,12月每个月有31天;4,6,9,114,6,9,11月每个月有30天;而对于22月,闰年时有29天,平年时有28天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:
1.这个年份是4的整数倍,但不是100的整数倍;
2.这个年份是400的整数倍。
例如:
•以下几个年份都是闰年:2000,2012,20162000,2012,2016。
•以下几个年份是平年:1900,2011,20141900,2011,2014。
输入
两行,每行包括一个8位数字。
第一行表示牛牛指定的起始日期。
第二行表示牛牛指定的终止日期。
保证date_i和都是真实存在的日期,且年份部分一定为4位数字,且首位数字不为0。
保证date 1 —定不晚于date 2。
输出
一个整数,表示在date1和date2之间,有多少个日期是回文的。
样例输入
20110101
20111231
样例输出
1
提示
样例说明】
对于样例1,符合条件的日期是20111102。
对于样例2,符合条件的日期是20011002和20100102。
【子任务】
对于%60的数据,满足date1 = date2
分析:首先看到这样的输入样例是有点蒙的,所以我的想法是先将输入的date进行拆分,拆成year,month和day;判断是否回文,只需要判断月日的逆序值是否等于年份即可,所以我的做法是让日期日增,来实现。这种做法很笨重也很容易出错,但未涉及任何算法知识。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int date1,date2,t;
scanf("%d%d",&date1,&date2);
int year1,month1,day1,year2,month2,day2;
year1=date1/10000;//下面是拆分日期
day1=date1%100;
month1=(date1%10000)/100;
year2=date2/10000;
day2=date2%100;
month2=(date2%10000)/100;
int item=0;
if(date1!=date2)
{
while(1)//循环让日期滚动
{
if(year1==day1%10*1000+day1/10*100+month1%10*10+month1/10)
{
item++;
day1++;
}
else
{
day1++;
if(month1==1||month1==3||month1==5||month1==7||month1==8||month1==10||month1==12)
{
if(day1>31)
{
month1++;
day1=1;
}
}
else if(month1==4||month1==6||month1==9||month1==11)
{
if(day1>30)
{
month1++;
day1=1;
}
}
else if(month1==2)
{
if(year1%400==0||(year1%4==0&&year1%100!=0))
{
if(day1>29)
{
month1++;
day1=1;
}
}
else if(day1>28)
{
month1++;
day1=1;
}
}
if(month1>12)
{
year1++;
month1=1;
}
}
if(year2==day2%10*1000+day2/10*100+month2%10*10+month2/10) //判断是否为回文
item++;
if(year1==year2&&month1==month2&&day1==day2) //日期相等时退出
break;
}
}
else
{
if(year1==day1%10*1000+day1/10*100+month1%10*10+month1/10)
{
item++;
}
}
printf("%d",item);
return 0;
}
但显然这种方法并不好,费时费力且容易出错,参考了林姐的题解后十分震撼,也感觉到了很大的差距。
使用枚举,并且在日期判断上,可以直接认为2月是29天,因为0229对应的9220正好是闰年,所以无需判断闰平年。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int month[13]={0,31,29,31,30,31,30,31,31,30,31,30,31};
int date1,date2;
int num=0;
int flag;
int sum;
scanf("%d%d",&date1,&date2);
for(int i=1;i<=12;i++)
{
for(int j=1;j<=month[i];j++)
{
flag=(j%10)*1000+(j/10)*100+(i%10)*10+i/10;
sum=flag*10000+i*100+j;
if(sum<date1||sum>date2)
continue;
num++;
}
}
printf("%d",num);
return 0;
}
问题E:求和(待解决)
题目描述
一条狭长的纸带被均匀划分出了n个格子,格子编号从1到n。每个格子上都染了一种颜色color_i用[1,m]当中的一个整数表示,并且写了一个数字number_i。

定义一种特殊的三元组:(x,y,z),其中x,y,z 都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:
xyz是整数,x<y<z,y-x=z-y
colorx=colorz
满足上述条件的三元组的分数规定为(x+z) *(number_x+number_z)。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大,你只要输出整个纸带的分数除以10,007所得的余数即可。
输入
第一行是用一个空格隔开的两个正整数n和m,n表纸带上格子的个数,m表纸带上颜色的种类数。 第二行有n用空格隔开的正整数,第i数字number表纸带上编号为i格子上面写的数字。 第三行有n用空格隔开的正整数,第i数字color表纸带上编号为ii格子染的颜色。
输出
共一行,一个整数,表示所求的纸带分数除以 10,007 所得的余数。
样例输入
6 2
5 5 3 2 2 2
2 2 1 1 2 1
样例输出
82
提示
【输入输出样例 说明】
纸带如题目描述中的图所示。
所有满足条件的三元组为:(1,3,5),(4,5,6)。
所以纸带的分数为(1+5)∗(5+2)+(4+6)∗(2+2) = 42+40 = 82。
【数据说明】
对于第 1 组至第 2 组数据, 1 ≤ n ≤ 100, 1 ≤ m ≤ 5,
对于第3 组至第 4 组数据, 1 ≤ n ≤ 3000, 1 ≤ m ≤ 100
对于第 5 组至第6组数据, 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000且不存在出现次数超过20的颜色;
对 于 全 部 10 组 数 据 , 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000,1≤color_i≤m,1≤number_i≤100000
看到这个题很崩溃的,完全超过了我的能力上限,甚至题目都难以读懂,大神们的题解也是看了非常非常久。
这个问题主要是在于数学的推导过程,由题意z-y=y-x,可化为z+x=2y,因此,z与x的奇偶性一定是相同的,又因为color_x=color_z故可以利用这两个特点,将奇偶性和颜色都相同的放入二维数组中。
而数学的推导过程:三元组是(x+z)(number_x+number_z),故其总分可以看作是ni与其他满足条件的编号的组合之和。编号n1与其他的组合可以写为(n1+n2)(num1+num2)+(n1+n3)(m1+m3)+...+(n1+ni)(m1+mi)=(n1 * m1+n1 * m2+n2 * m1+n2 * m2)+(n1 * m1+n1 * m3+n3 * m1+n3 * m3)+...+(n1 * m1+n1 * mi+ni * m1+ni * mi)每个括号的前两项可以提出来变成n1 * Σm_i+(i-2)∑(n_i * m_i),而后两项则可以单独拿出与编号n2与其他组合的化简式后两项组合,最终所有的能合成Σi * sum+(i-2) * Σ(i * m_i);过程中不要忘记%10007.
#include<bits/stdc++.h>
using namespace std;
long long num[100005];
long long colsum[100005][2];
long long sum[100005][2];
long long color[100005][2];
long long col[100005];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
long long result=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&num[i]);
}
for(int i=1;i<=n;i++)
{
scanf("%lld",&col[i]);
color[col[i]][i%2]++;
colsum[col[i]][i%2]=(colsum[col[i]][i%2]+num[i])%10007;
}
for(int i=1;i<=n;i++)
{
result=(result+i*colsum[col[i]][i%2]+(color[col[i]][i%2]-2)*i*num[i]%10007)%10007;
}
printf("%lld",result);
}
在最后提交的时候,洛谷提交了很多遍,但是都没有完全通过,后来将int全部改为long long 才完全通过的。
问题F:推销员(待解决)
问题G:扫雷
题目描述
扫雷游戏是一款十分经典的单机小游戏。在 n 行 m 列的雷区中有一些格子含有地雷 (称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩家翻开一个非地雷格时, 该格将会出现一个数字——提示周围格子中有多少个是地雷格。游戏的目标是在不翻出 任何地雷格的条件下,找出所有的非地雷格。 现在给出n行m列的雷区中的地雷分布,要求计算出每个非地雷格周围的地雷格数。
注:一个格子的周围格子包括其上、下、左、右、左上、右上、左下、右下八个方 向上与之直接相邻的格子。
输入
输入文件第一行是用一个空格隔开的两个整数n和m,分别表示雷区的行数和列数。 接下来 n 行,每行 m 个字符,描述了雷区中的地雷分布情况。字符’*’表示相应 格子是地雷格,字符’?’表示相应格子是非地雷格。相邻字符之间无分隔符。
输出
输出文件包含 n 行,每行 m 个字符,描述整个雷区。用’*’表示地雷格,用周围 的地雷个数表示非地雷格。相邻字符之间无分隔符。
样例输入
3 3
??
???
??
样例输出
10
221
11
提示
【数据说明】 对于 100%的数据,1≤n≤100,1≤m≤100。
分析:这个题,还是菜,只能用最笨的方法去做,一个一个去判断八种不同的位置。
#include<bits/stdc++.h>
using namespace std;
int main()
{
char a[100][101];
int cle,row,i,k,lei;
scanf("%d%d",&row,&cle);
for(i=0;i<row;i++)
{
scanf("%s",a[i]);
}
for(i=0;i<row;i++)
{
for(k=0;k<cle;k++)
{
lei=0;
if(a[i][k]=='*') printf("%c",'*');
else{
if(a[i-1][k-1]=='*') lei++;
if(a[i-1][k]=='*') lei++;
if(a[i-1][k+1]=='*') lei++;
if(a[i][k-1]=='*') lei++;
if(a[i][k+1]=='*') lei++;
if(a[i+1][k-1]=='*') lei++;
if(a[i+1][k]=='*') lei++;
if(a[i+1][k+1]=='*') lei++;
printf("%d",lei);
}
}
printf("\n");
}
return 0;
}
问题H买铅笔
题目描述
P老师需要去商店买n支铅笔作为小朋友们参加NOIP的礼物。她发现商店一共有 33种包装的铅笔,不同包装内的铅笔数量有可能不同,价格也有可能不同。为了公平起 见,P老师决定只买同一种包装的铅笔。
商店不允许将铅笔的包装拆开,因此P老师可能需要购买超过n支铅笔才够给小朋 友们发礼物。
现在P老师想知道,在商店每种包装的数量都足够的情况下,要买够至少n支铅笔最少需要花费多少钱。
输入
第一行包含一个正整数n,表示需要的铅笔数量。
接下来三行,每行用2个正整数描述一种包装的铅笔:其中第1个整数表示这种 包装内铅笔的数量,第2个整数表示这种包装的价格。
保证所有的7个数都是不超过10000的正整数。
输出
1个整数,表示P老师最少需要花费的钱。
样例输入
57
2 2
50 30
30 27
样例输出
54
提示
铅笔的三种包装分别是:
22支装,价格为2;
5050支装,价格为30;
3030支装,价格为27。
P老师需要购买至少57支铅笔。
如果她选择购买第一种包装,那么她需要购买29份,共计2 * 29=58支,需要花费的钱为2 * 29 = 58。
实际上,P老师会选择购买第三种包装,这样需要买2份。虽然最后买到的铅笔数 量更多了,为30 * 2 = 60支,但花费却减少为27 * 2 = 54,比第一种少。
对于第二种包装,虽然每支铅笔的价格是最低的,但要够发必须买2份,实际的花费达到了 30 * 2 = 60,因此P老师也不会选择。
所以最后输出的答案是54。
分析:这个题非常简单,包装不能拆,且只能买同一种,所以只需要将三种情况完全求出来,在比较输出最小的一种方案即可。
#include<stdio.h>
int main()
{
int n,x1,p1,x2,p2,x3,p3,a,b,c,min;
scanf("%d%d%d%d%d%d%d",&n,&x1,&p1,&x2,&p2,&x3,&p3);
if(n%x1==0)
{
a=p1*(n/x1);
}
else a=p1*(n/x1+1);
if(n%x2==0)
{
b=p2*(n/x2);
}
else b=p2*(n/x2+1);
if(n%x3==0)
{
c=p3*(n/x3);
}
else c=p3*(n/x3+1);
min=b;
if(a<b) min = a;
if(min>c) min = c;
printf("%d",min);
}
总结一下集训队第二次周赛,这是我加入acm以来的第一次训练赛,高强度的训练和做题身体有点被掏空的感觉,但我知道这些题只不过是acm竞赛中的入门题目,让我认识到自身从基础语法到算法上的不足,并参考了林姐等大佬的博客后,从思路和解题方法上认识到了自身的差距,因此,要更加努力去追赶,发现不足,并抓住知识盲点进行突破。
年轻的心是被梦想撑大的!!!
