素数筛,埃式素数筛,欧拉素数筛
素数筛
怎么找到从2 ~ n 的所有素数,回忆起一开始刚开始学习编程的时候,用的是最暴力的方法,从2 ~ n枚举,再对这个数(暂取x)除以2~x,如果都无法除尽,那么这个数就是素数。
后来知道可以不用取到x,到二分之一就可以,再后来知道 到根号x就可以。
但是这样依然很麻烦,复杂度非常高,所以便了解到了埃式素数筛。
埃式筛法
要求:依次输出从 2 ~ n 的所有素数。
思路,我们都知道2是最小的素数,那就从2开始,让他去乘一个数 i ,一直到 i*2 大于n的时候,中间得到的这些乘积就都是合数了,直接从bool类型数组中剔除,然后再是 3 .。。。一直到n。
代码实现:
bool Prime[1000010];//这里上限设置的是1000010;
void isPrime()
{
memset(Prime,true,sizeof(Prime));
for(int i=2;i<=1000010;i++)
{
for(int j=2;j*i<=1000010;j++)
{
Prime[j*i]=false;
}
}
}
但很快,人们就发现,这种筛选方法还不够完美(尽管已经很快了),因为一个合数有可能被筛选了很多遍,举个例子 6.
在 i = 2,j = 3 时,筛掉了一遍
在 i = 3,j = 2 时,又筛掉了一遍
如果数更大的话,那就会被筛掉更多变,于是,便有了欧拉筛法。
欧拉筛法
真的很佩服这些算法科学家,我们看都看不懂的东西,他们竟然会从无到有的建立。。。像极了科(ai)学(qing)。。。
如何保证一个合数只被筛掉一遍?关键点在于。
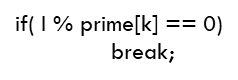
借用一下鹏哥的笔记
分析过程
假设 xy = ab,其中 x,a 为质数,那么有 x | b , a | y.
例如:
26 = 34
2 | 4 , 3 | 6
引理2:
任何一个合数都可以表示成一个质数和一个整数的乘积。
对于一个合数 A
①如果 A 只能分解成一个 素数整数 的形式,那么这个整数必为素数,这也就意味着 i 为素数;
那么 if( i%prime[j] == 0) 始终为false.
例如:假设A=21=37
当 i = 7 是,会与之前求出的所有的素数相乘,使得 isPirme[ iprime[j] ] =false
那么对于所有的只能分解成 素数素数 形式的合数会全部筛去。
②如果 A 可以分解成多个 素数合数 的形式
不妨假设 A = a1b1 = a2b2 ,并且 a1,a2为素数,a1 < a2;
那么由引理1可得
a1 | b2 , a2 | b1
由于 a1 < a2,所以 b1 > b2,
当 i = b2时,在执行完 prime[ a1b2 ]=false 后,一定会执行 if( b2%a1 == 0) 这条语句,
那么就不会执行 prime[ a2*b2 ]=false 这条语句。
其中2|4的意思是2能被4整除
代码实现:
int Prime[1000010];
bool visit[1000010];
int cont=0;
int sign[1000010]={0};
void isPrime()
{
memset(visit,true,sizeof(visit));
memset(Prime,0,sizeof(Prime));
visit[1]=false;
for(int i=2;i<1000010;i++)
{
if(visit[i])
Prime[cont++]=i;
for(int j=0;j<cont&&i*Prime[j]<=1000010;j++)
{
cout<<" j = "<<j<<" prime["<<j<<"]"<<" = "<<prime[j]<<" i*prime[j] = "<<i*prime[j]<<endl;//可以看一下被筛走的过程。
visit[i*Prime[j]]=false;
if(i%Prime[j]==0)
break;
}
}
}
