（一）树状数组

模型1：改点求段

数据的储存状态：

精髓操作：

int lowbit(int x)
{
    return (x&(-x));
}

操作规律：向上修改，向下查找。

void add(int pos,int x)
{
    for(int i=pos;i<=n;i+=lowbit(i))
    {
        a[i]+=x;
    }
}
long long query(int pos)
{
    long long ans=0;
    for(int i=pos;i>0;i-=lowbit(i))
    {
        ans+=a[i];
    }
    return ans;
}

例题1：见上次博客，敌兵布阵

模型2：改段求点

设置一个d[n]数组（也叫做差分数组），用来储存d[i]=a[i]-a[i-1]，易证得a[i]=d[i]+d[i-1]+d[i-2]+···+d[2]+d[1];
对于区间修改我们举这样一个例子：a[]={2,5,4,3,10,8};其对应的差分数组为b[]={2,3,-1,-1,7,-2}，对a的1-4做+2操作得到a[]={2,7,6,5,12,8},其对应差分数组变为b[]={2,5,-1,-1,7,-4}我们发现改变的也同样只有1，5两位，故可以将差分数组存入一个树状数组中，区间修改就变成了单点修改，而单点查询变成了求前缀和。

精髓操作：

int lowbit(int x)
{
    return (x&(-x));
}

维护差分数组：

void dadd(int pos,int x)
{
    for(int i=pos;i<=n;i+=lowbit(i))
    {
        a[i]+=x;
    }
}

求a[i]即求d[]的前i项和

long long query(int pos)
{
    long long ans=0;
    for(int i=pos;i>0;i-=lowbit(i))
    {
        ans+=a[i];
    }
    return ans;
}

例题2：洛谷P3368 树状数组2

题目描述
如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的值

输入格式
第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1：格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2：格式：2 x 含义：输出第x个数的值

输出格式
输出包含若干行整数，即为所有操作2的结果。

输入输出样例
输入

输出

6
10

说明
时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

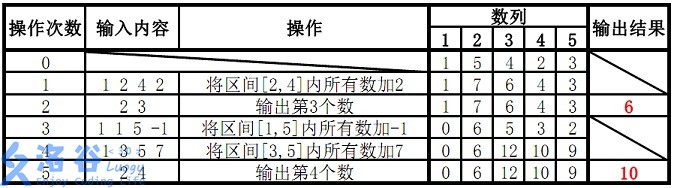
故输出结果为6、10

#include<bits/stdc++.h>
using namespace std;
const int MAXN=500000+50;
int n;
long long d[MAXN];
long long a[MAXN];
long long tree[1000000];
int lowbit(int x)
{
    return (x&(-x));
}
void dadd(int pos,int x)
{
    for(int i=pos;i<=n;i+=lowbit(i))
    {
        tree[i]+=x;
    }
}
long long query(int pos)
{
    long long ans=0;
    for(int i=pos;i>0;i-=lowbit(i))
    {
        ans+=tree[i];
    }
    return ans;
}
int main()
{
    int m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        if(i==1)
            d[i]=a[i];
        else
            d[i]=a[i]-a[i-1];
    }
    for(int i=1;i<=n;i++)
    {
        dadd(i,d[i]);
    }
    while(m--)
    {
        int cmd,x,y,k;
        cin>>cmd;
        if(cmd==1)
        {
            cin>>x>>y>>k;
            dadd(x,k);
            dadd(y+1,-k);
        }
        else
        {
            cin>>k;
            cout<<query(k)<<'\n';
        }
    }
    return 0;
}

模型3：改段求段（线段树）

与 2 中类似, 先开一个差分数组 d

那么有:

a1 + a2 + ... + an

= d1 + (d1 + d2) + ... + (d1 + d2 + ... + dn)

= n _ d1 + (n - 1) _ d2 + ... + dn

= n _ (d1 + d2 + ... + dn) - (0 _ d1 + 1 _ d2 + ... (n - 1) _ dn)
再令c[i] = ( i - 1)* di

那么原式可化简为:

n * (d1 + d2 + ... + dn) - (c1 + c2 + ... cn)

例题3

题目描述 Description
给你N个数，有两种操作：
1：给区间[a,b]的所有数增加X
2：询问区间[a,b]的数的和。
输入描述 Input Description
第一行一个正整数n，接下来n行n个整数，
再接下来一个正整数Q，每行表示操作的个数，
如果第一个数是1，后接3个正整数，
表示在区间[a,b]内每个数增加X,如果是2，
表示操作2询问区间[a,b]的和是多少。
pascal选手请不要使用readln读入
输出描述 Output Description
对于每个询问输出一行一个答案
样例输入 Sample Input

样例输出 Sample Output

数据范围及提示 Data Size & Hint
数据范围

1<=n<=200000

1<=q<=200000

AC代码：

#include<bits/stdc++.h>
using namespace std;
const long long MAXN=500000+50;
long long n;
long long a[MAXN],d[MAXN],c[MAXN];
long long lowbit(long long x)
{
    return (x&(-x));
}
void add(long long *tree,long long pos,long long x)
{
    for(long long i=pos;i<=n;i+=lowbit(i))
    {
        tree[i]+=x;
    }
}
long long query(long long *tree,long long pos)
{
    long long ans=0;
    for(long long i=pos;i>0;i-=lowbit(i))
    {
        ans+=tree[i];
    }
    return ans;
}
int main()
{
    cin>>n;

    for(long long i=1;i<=n;i++)
    {
        cin>>a[i];
        add(d,i,a[i]-a[i-1]);
        add(c,i,(i-1)*(a[i]-a[i-1]));
    }
    long long q;
    cin>>q;
    while(q--)
    {
        long long cmd;
        cin>>cmd;
        if(cmd==1)
        {
            long long x,y,k;
            cin>>x>>y>>k;
            add(d,x,k);
            add(d,y+1,-k);
            add(c,x,(x-1)*k);
            add(c,y+1,-k*y);
        }
        else
        {
            long long x,y;
            cin>>x>>y;
            cout<<(y*(query(d,y))-query(c,y)-((x-1)* query(d,x-1)-query(c,x-1)))<<'\n';
        }
    }
}

（二）RMQ算法

用法，用于查询区间最值的算法，max[i][j]数组的意义为，第i项到第i+2^{j项的最大值。

对于i~i+2}j-1这段区间，我们将它分为长度相同的两部分：

显然2^j=2(j-1)+2^{(j-1),所以分为i~i+2}(j-1)-1, i+2^(j-1)~i+2j-1；

那么f[i][j]=max/min(f[i][j-1],f[i+2^(j-1)][j-1])。

所以当查询一段区间[l,r]时：

Int k=log2(r-l+1);

Int ans=max/min(f[l][k],f[r-2^k+1][k]);

例题1：

Description

在每天挤奶的时候，农民约翰的N头牛（1≤n≤50000）总是排成一列。有一天，约翰决定与他的牛们一起玩一个极限飞盘游戏。为了简单起见，他将从奶牛队列里面选一定范围内的奶牛来玩这个游戏。然而所有的牛对这个游戏都很感兴趣。农民约翰列出了Q份名单（1≤Q≤200000）和每个奶牛的高度（1≤高度≤1000000）。对于每一份名单，他想你帮助他确定在每份名单中高度最高的奶牛与高度最低的奶牛的高度差是多少。

Input

第一行为N(1≤N≤50000)和Q(1≤Q≤200000)；从第2行到第N+1行，每行一个数字，表示第i头牛的高度(1≤height≤1000000)；从第N+2行到第N+Q+1行，每行两个整数A和B(1≤A≤B≤N)，表示从第A头牛到第B头牛的范围。

Output

从第一行到第Q行，每行一个整数，表示从第A头牛到第B头牛之间，最高牛与最矮牛的高度差。
Sample Input

Sample Output

6
3
0

这RMQ的模板题，取区间最大-最小就是答案。
AC代码:

#include<bits/stdc++.h>
using namespace std;
const int MAXN=500000+50;
int Max[MAXN][20];
int Min[MAXN][20];
int n;
void rmq()
{
    for(int j=1;j<=20;j++)
    {
        for(int i=1;i<=n;i++)
        {
            if(i+(1<<j)-1<=n)
            {
                Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
                Min[i][j]=min(Min[i][j-1],Min[i+(1<<(j-1))][j-1]);
            }
        }
    }
}
int main()
{
    int q;
    cin>>n>>q;
    for(int i=1;i<=n;i++)
    {
        cin>>Max[i][0];
        Min[i][0]=Max[i][0];
    }
    rmq();
    while(q--)
    {
        int l,r;
        cin>>l>>r;
        int k=log2(r-l+1);
        int ans1;
        int ans2;
        ans1=max(Max[l][k],Max[r-(1<<k)+1][k]);
        ans2=min(Min[l][k],Min[r-(1<<k)+1][k]);
        cout<<ans1-ans2<<'\n';
    }
    return 0;
}

例题2：HDU1806.Frequent values

Description

给你一个含有n个整数的非递减序列a1 , a2 , ... , an，要求你回答一系列的询问，如i和j (1 ≤ i ≤ j ≤ n)，回答出ai , ... , aj之间出现频率最多数字为多少次？

Input

输入文件包含多组数据，每组数据的第1行包含两个整数n和q(1 ≤ n, q ≤ 100000)，第2行为n个用空格分开的整数a1 , ... , an (-100000 ≤ ai ≤ 100000, for each i ∈ {1, ..., n})，接下来的q行，每行包含两个整数i和j。文件以0作为结束标记。
Output

对于每一个询问输出一行，为在此区间内出现频率最多数字为多少次？

Sample Input

    10 3
    -1 -1 1 1 1 1 3 10 10 10
    2 3
    1 10
    5 10
    0

Sample Output

    1
    4
    3

Hint
【数据范围】

    对于30的数据，1≤n,q≤1000；
    对于100的数据，1≤n,q≤1000000;

l数组是用来记录当前这个字符是所在连续字符的第几个，如样例中的数字是
a[]={-1,-1, 1, 1, 1, 1, 3,10,10,10}，那么与其对应的
l[]={ 1, 2, 1, 2, 3, 4, 1, 1, 2, 3}，这样便成为了查找l[]区间最值的问题，需要注意的是，区间内的数字不一定是完整的（区间内只有一个数字），所以需要先判断一下，区间中是否完全是一个数，若完整，则直接输出e-s+1（即区间中数字个数）。
若不完整，则需要进行分类讨论，从区间前半段（都为开头的那一个数字），和后半段（剩下的数字）中取区间最大值，然后二者再进行比较。

    #include<bits/stdc++.h>
    using namespace std;
    const int MAXN=100000+50;
    int a[MAXN],l[MAXN],Max[MAXN][20];
    int n;
    void getst()//rmq的ST表
    {
        for(int j=1;j<=20;j++)
        {
            for(int i=1;i<=n;i++)
            {
                if(i+(1<<j)-1<=n)
                {
                    Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
                }
            }
        }
    }
    int rmq(int l,int r)//rmq获取答案
    {
        int k=log2(r-l+1);
        return max(Max[l][k],Max[r-(1<<k)+1][k]);
    }
    int main() {
        ios::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
        while(cin>>n&&n!=0)
        {
            int q;
            cin>>q;
            memset(Max,0,sizeof(Max));
            a[0]=100005;
            for(int i=1;i<=n;i++)
            {
                cin>>a[i];
                if(a[i]==a[i-1])
                {
                    l[i]=l[i-1]+1;
                    Max[i][0]=l[i];//ST表初始化
                }
                else
                {
                    l[i]=1;
                    Max[i][0]=l[i];//ST表初始化
                }
            }
            getst();
            while(q--)
            {
                int s,e;
                cin>>s>>e;
                int t=s;
                while(a[t]==a[t-1]&&t<=e)//判断区间内是否只有一个数字
                t++;
                if(t>e)//如果区间内都为一个数字
                cout<<e-s+1<<'\n';//输出区间内数字个数
                else{
                    cout<<max(rmq(t,e),t-s)<<'\n';//讨论前缀，与后缀最大值，的大小
                }
            }
        }
        return 0;
    }

省赛前算法复习笔记(一)