哈理工训练赛20190310团队赛
第一次参加团队赛,非常感谢我的队友,丁智辰和刘少瑞
A - Coffee Break
Recently Monocarp got a job. His working day lasts exactly m minutes. During work, Monocarp wants to drink coffee at certain moments: there are n minutes a1,a2,…,an, when he is able and willing to take a coffee break (for the sake of simplicity let's consider that each coffee break lasts exactly one minute).
However, Monocarp's boss doesn't like when Monocarp takes his coffee breaks too often. So for the given coffee break that is going to be on minute ai, Monocarp must choose the day in which he will drink coffee during the said minute, so that every day at least d minutes pass between any two coffee breaks. Monocarp also wants to take these n coffee breaks in a minimum possible number of working days (he doesn't count days when he is not at work, and he doesn't take coffee breaks on such days). Take into account that more than d minutes pass between the end of any working day and the start of the following working day.
For each of the n given minutes determine the day, during which Monocarp should take a coffee break in this minute. You have to minimize the number of days spent.
Input
The first line contains three integers n, m, d (1≤n≤2⋅105,n≤m≤109,1≤d≤m) — the number of coffee breaks Monocarp wants to have, the length of each working day, and the minimum number of minutes between any two consecutive coffee breaks.
The second line contains n distinct integers a1,a2,…,an (1≤ai≤m), where ai is some minute when Monocarp wants to have a coffee break.
Output
In the first line, write the minimum number of days required to make a coffee break in each of the n given minutes.
In the second line, print n space separated integers. The i-th of integers should be the index of the day during which Monocarp should have a coffee break at minute ai. Days are numbered from 1. If there are multiple optimal solutions, you may print any of them.
Input
4 5 3
3 5 1 2
Output
3
3 1 1 2
Input
10 10 1
10 5 7 4 6 3 2 1 9 8
Output
2
2 1 1 2 2 1 2 1 1 2
Note
In the first example, Monocarp can take two coffee breaks during the first day (during minutes 1 and 5, 3 minutes will pass between these breaks). One break during the second day (at minute 2), and one break during the third day (at minute 3).
In the second example, Monocarp can determine the day of the break as follows: if the minute when he wants to take a break is odd, then this break is on the first day, if it is even, then this break is on the second day.
待解决
TLE代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
struct ca
{
int a;
int b;
long long int flag;
}c[200000];
bool c1(ca cc1,ca cc2)
{
return cc1.a<cc2.a;
}
bool c2(ca cc1,ca cc2)
{
return cc1.b<cc2.b;
}
int main()
{
int n,m,d,i,sum=0;
scanf("%d%d%d",&n,&m,&d);
for(i=1;i<=n;i++)
{
scanf("%d",&c[i].a);
c[i].b=i;
c[i].flag=0;
}
sort(c+1,c+n+1,c1);
long long day=0;
while(sum!=n)
{
day++;
int time=0;
for(i=1;i<=n;i++)
{
if(time>m)
{
break;
}
if(c[i].flag==0&&c[i].a>=time)
{
c[i].flag=day;
time=c[i].a+1+d;
sum++;
}
}
}
sort(c+1,c+n+1,c2);
printf("%d\n",day);
for(i=1;i<=n;i++)
{
printf("%d ",c[i].flag);
}
return 0;
}
C - Bacteria
Recently Monocarp has created his own mini-laboratory!
The laboratory contains n bacteria. Monocarp knows that he can merge any two bacteria having equal sizes, and the resulting bacterium will have the size equal to the sum of sizes of merged bacteria. For example, if two bacteria having sizes equal to 7 merge, one bacterium with size 14 is the result.
It becomes hard to watch for many bacteria, so Monocarp wants to merge all of them into one bacterium. It may not be possible to do this with the bacteria Monocarp has, so he can buy any number of bacteria of any possible integer sizes in a special store.
You have to determine the minimum number of bacteria Monocarp has to buy to merge them with the n bacteria his laboratory contains into exactly one bacterium.
Input
The first line contains one integer n (1≤n≤2⋅105) — the number of bacteria Monocarp's laboratory contains.
The second line contains n integers a1,a2,…,an (1≤ai≤109), where ai is the size of the i-th bacterium in the laboratory.
Output
If it is impossible to merge the bacteria (possibly after buying some) into only one bacterium, print -1.
Otherwise print the minimum number of bacteria Monocarp has to buy to merge them with the n bacteria his laboratory contains into exactly one bacterium.
Input
2
1 4
Output
2
Input
3
3 6 9
Output
-1
Input
7
1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
Output
1
Note
In the first example Monocarp should buy one bacterium having size 1 and one bacterium having size 2. Then Monocarp will have 4 bacteria having sizes [1,4,1,2]. Then two bacteria having sizes 1 can be merged into one having size 2. Then Monocarp will have 3 bacteria having sizes [2,4,2]. Then two bacteria having sizes 2 can be merged into one having size 4. Then Monocarp will have 2 bacteria having sizes [4,4], which can be merged into one having size 8.
In the second example no matter which bacteria Monocarp will buy, he cannot merge all his bacteria.
In the third example Monocarp needs to buy one bacterium having size 1000000000.
题意:有n个大小不同的菌落,两个大小相同的菌落可以进行合并,如果没有相同的菌落,则需要去购买菌落再合并,一直合并到只有一个菌落为止,如果无法完全合并成一个菌落,则输出-1,否则输出购买的次数。
思路:首先我们要把这些菌落的数目进行排序,最小的两个进行合并,但是合并完又要进行依次排序,所以我就想到了使用优先队列,每次取出最顶端的两个进行操作,操作完再放入优先队列。然后就是怎么判断能否合并完全的问题了(也是难点)。
首先我们要判断取出的x,y(x<y)是否相同,相同直接合并并存入队列,如果不相同,那么y是否是x的偶数倍(具体是怎么想到的也忘记了,好像就是举了几个例子:(1,4 )(3,9)。。。)除了这两种情况就可以直接输出-1了,而需要购买的次数也是通过举例抽取出的(1,4)(1,8)。
AC代码:
#include<bits/stdc++.h>
using namespace std;
priority_queue<long long,vector<long long>,greater<long long> >que;
int main()
{
long long n;
cin>>n;
long long a;
for(int i=0;i<n;i++)
{
cin>>a;
que.push(a);
}
long long x,y;
long long ans=0;
int flag=1;
while(que.size()>1)
{
x=que.top();
que.pop();
y=que.top();
que.pop();
if(x==y)
{
que.push(2*y);
}
else if(y%x!=0||((y/x)%2!=0))
{
flag=0;
cout<<-1;
break;
}
else
{
int z=y/x;
while(z!=1)
{
z/=2;
ans++;
}
que.push(y*2);
}
}
if(flag==1)
cout<<ans;
return 0;
}
H - Theater Square
The Theater Square can be represented as a rectangle having height n and length m, divided into square 1×1 cells. Let's denote the cell located at the intersection of i-th row and j-th column as (i,j). The rows are numbered from top to bottom, the columns — from left to right.
There is a rectangular fountain inside the Teather Square. The cell in its left upper corner is (x1,y1), the cell in its right lower corner is (x2,y2).
The Theater Square soon will be paved with tiles having height 1 and length 2. Every cell (except cells inside the fountain) should be paved, and no cell should be covered by more than one tile. All tiles will be laid out horizontally, so the cells covered by each tile are in the same row. To pave the whole Theater Square it might be necessary to break some tiles. After breaking a tile, two new tiles of size 1×1 are formed (which cannot be broken further). You may consider that the mayor, who ordered the paving of the Theater Square, has infinite number of tiles 1×2.
Since broken tiles are not beautiful, among all possible ways to pave the Theater Square the mayor wants to choose a way such that the number of tiles to be broken into two lesser tiles is minimum possible. Pay attention that tiles should be laid horizontally, no tile can cover cells in different rows.
Help the mayor! Tell him the minimum possible number of tiles to be broken.
Input
The first line contains two integers n and m (1≤n,m≤2⋅105) — the height and the length of the Theater Square, respectively.
The second line contains four numbers x1,y1,x2,y2 (1≤x1≤x2≤n,1≤y1≤y2≤m) — the coordinates of left upper corner and right lower corner of the fountain.
Output
Print one number — minimum possible number of tiles mayor has to break in order to pave the whole Theater Square.
Input
6 5
1 2 3 4
Output
5
Input
6 1
3 1 4 1
Output
2
Input
1 12
1 3 1 8
Output
0
Note
One of the optimal ways to pave the Theater Square in the first example:
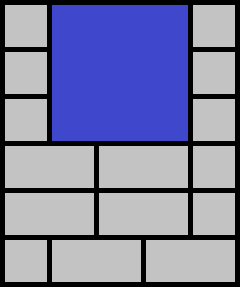
5 tiles are to be broken.
AC代码(lsr):
#include <cstdio>
using namespace std;
int main(){
long long h,l,x1,x2,y1,y2,h1,a,b,c,sum,ans;
scanf("%lld%lld%lld%lld%lld%lld",&h,&l,&y1,&x1,&y2,&x2);
h1=y2-y1+1;
a=((x1-1)%2)*h1;
b=((l-x2)%2)*h1;
c=(h-h1)*(l%2);
sum=a+b+c;
ans=sum/2;
ans+=(sum%2);
printf("%lld",ans);
return 0;
}
I - Heist
There was an electronic store heist last night.
All keyboards which were in the store yesterday were numbered in ascending order from some integer number x. For example, if x=4 and there were 3 keyboards in the store, then the devices had indices 4, 5 and 6, and if x=10 and there were 7 of them then the keyboards had indices 10, 11, 12, 13, 14, 15 and 16.
After the heist, only n keyboards remain, and they have indices a1,a2,…,an. Calculate the minimum possible number of keyboards that have been stolen. The staff remember neither x nor the number of keyboards in the store before the heist.
Input
The first line contains single integer n (1≤n≤1000) — the number of keyboards in the store that remained after the heist.
The second line contains n distinct integers a1,a2,…,an (1≤ai≤109) — the indices of the remaining keyboards. The integers ai are given in arbitrary order and are pairwise distinct.
Output
Print the minimum possible number of keyboards that have been stolen if the staff remember neither x nor the number of keyboards in the store before the heist.
Input
4
10 13 12 8
Output
2
Input
5
7 5 6 4 8
Output
0
Note
In the first example, if x=8 then minimum number of stolen keyboards is equal to 2. The keyboards with indices 9 and 11 were stolen during the heist.
In the second example, if x=4 then nothing was stolen during the heist.
题意:输入n个数,最小的和最大的之间,没有在输入中出现的数字的个数。
思路:发现了一个签到题,哇塞,我来kao,结果,tle了,实在太大意了,感谢dzc。
AC代码:
#include<bits/stdc++.h>
using namespace std;
long long a[1010];
int main()
{
int n;
cin>>n;
long long Max=0,Min=1000000000+1;
for(int i=0;i<n;i++)
{
cin>>a[i];
Max=max(Max,a[i]);
Min=min(Min,a[i]);
}
cout<<Max-Min-n+1;
return 0;
}
J - Buying a TV Set
Monocarp has decided to buy a new TV set and hang it on the wall in his flat. The wall has enough free space so Monocarp can buy a TV set with screen width not greater than a and screen height not greater than b. Monocarp is also used to TV sets with a certain aspect ratio: formally, if the width of the screen is w, and the height of the screen is h, then the following condition should be met: wh=xy.
There are many different TV sets in the shop. Monocarp is sure that for any pair of positive integers w and h there is a TV set with screen width w and height h in the shop.
Monocarp isn't ready to choose the exact TV set he is going to buy. Firstly he wants to determine the optimal screen resolution. He has decided to try all possible variants of screen size. But he must count the number of pairs of positive integers w and h, beforehand, such that (w≤a), (h≤b) and (wh=xy).
In other words, Monocarp wants to determine the number of TV sets having aspect ratio xy, screen width not exceeding a, and screen height not exceeding b. Two TV sets are considered different if they have different screen width or different screen height.
Input
The first line contains four integers a, b, x, y (1≤a,b,x,y≤1018) — the constraints on the screen width and height, and on the aspect ratio.
Output
Print one integer — the number of different variants to choose TV screen width and screen height so that they meet the aforementioned constraints.
Input
17 15 5 3
Output
3
Input
14 16 7 22
Output
0
Input
4 2 6 4
Output
1
Input
1000000000000000000 1000000000000000000
999999866000004473 999999822000007597
Output
1000000063
Note
In the first example, there are 3 possible variants: (5,3), (10,6), (15,9).
In the second example, there is no TV set meeting the constraints.
In the third example, there is only one variant: (3,2).
题目大意:要去买电视,宽w不能超过a,高h不能超过b,a/b=x/y。求满足要求的所有情况。
思路:首先要把x/y约分,分别用对a,b整除化简后的x与y,并去最小,就是答案。
AC代码:
#include<bits/stdc++.h>
using namespace std;
long long Gcd(long long x,long long y)
{
return x==0?y:Gcd(y%x,x);
}
int main()
{
long long T;
long long a,b,x,y;
cin>>a>>b>>x>>y;
T=Gcd(x,y);
long long mina=x/T;
long long minb=y/T;
cout<<min(a/mina,b/minb);
return 0;
}
K - Medians and Partition
Let median of some array be the number which would stand in the middle of this array if it was sorted beforehand. If the array has even length let median be smallest of of two middle elements. For example, median of the array [10,3,2,3,2] is 3 (i.e. [2,2,3–,3,10]). Median of the array [1,5,8,1] is 1 (i.e. [1,1–,5,8]).
Let array be m-good if its median is greater or equal than m.
Let the partition of array [a1,a2,…,an] be a set of subarrays {b1,b2,…,bk} such that b1=[a1,a2,…,ai1], b2=[ai1+1,ai1+2,…,ai2], ..., bk=[aik−1+1,aik−1+2,…,an]. For example, array [10,3,2,3,2] can be partitioned as follows: {[10,3,2,3,2]} or {[10],[3],[2],[3],[2]}, or {[10],[3,2,3,2]}, or {[10,3],[2],[3,2]} and so on.
You are given array a of length n and integer m. Find the partition of a into maximum number of subarrays such that each subarray is m-good.
Input
The first line contains two integers n and m (1≤n≤5000, 1≤m≤5000) — length of array a and constant m.
The second line contains n integers a1, a2, ..., an (1≤ai≤5000)— array a.
Output
If there is no valid partition of array a into m-good subarrays, print 0. Otherwise print maximum number of subarrays in partition of array a such that each subarray is m-good.
Input
5 2
10 3 2 3 2
Output
5
Input
5 3
10 3 2 3 2
Output
1
Input
5 4
10 3 2 3 2
Output
0
lsr大佬的AC代码:
具体做法思路待更新
#include<bits/stdc++.h>
using namespace std;
int n,m,x,ans;
int main(){
scanf("%d%d",&n,&m);
ans=0;
for(int i=0;i<n;i++){
scanf("%d",&x);
if(x>=m) ans++;
else ans--;
}
if(ans<0) ans=0;
printf("%d",ans);
return 0;
}
第一场训练赛就这样结束了,整个过程的提交失败卡的很难受,以前觉得最恐怖的是wa,后来是tle再后来就是现在的sf😂。难忘今宵
