中石油 2019年春季个人训练赛第二场 2019-3-1
问题 D: 组合数问题I
题目描述
组合数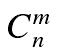 表示的是从n个物品中选出m个物品的方案数。举个例子,从(1,2,3)三个物品中选择两个物品可以有(1, 2), (1, 3), (2, 3)这三种选择方法。根据组合数的定义,我们可以给出计算组合数 的一般公式:
表示的是从n个物品中选出m个物品的方案数。举个例子,从(1,2,3)三个物品中选择两个物品可以有(1, 2), (1, 3), (2, 3)这三种选择方法。根据组合数的定义,我们可以给出计算组合数 的一般公式: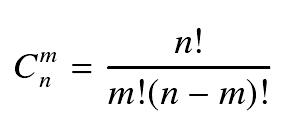
其中n! = 1×2×...×n。
小葱想知道如果给定n, m和k,对于所有的0≤i≤n,0≤ j≤min(i,m)有多少对(i, j)满足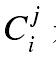 是k的倍数。
是k的倍数。
输入
第一行有两个整数t, k,其中t代表该测试点总共有多少组测试数据,k的意义见【问题描述】。接下来t行每行两个整数n, m,其中n, m的意义见【问题描述】。
输出
t行,每行一个整数代表所有的。0≤i≤n,0≤ j≤min(i,m)有多少对(i, j)满足是k的倍数。
样例输入
1 2
3 3
样例输出
1
提示
在所有可能的情况中,只有以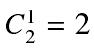 是2的倍数。3≤n,m≤2000,2≤k≤21,1≤t≤10000
是2的倍数。3≤n,m≤2000,2≤k≤21,1≤t≤10000
** 组合数递推+取模+前缀和**
思路:如果是想用阶乘来暴力求解的话,显然是不现实的。所以考虑算法,这个数学问题高中有所涉及,但是我也忘记了,于是现推公式c [i , j]=c [i - 1, j] + c [ i - 1, j - 1 ],当然,比较简单的思考方法是杨辉三角。于是我们便可以把组合数结果打出表来了,记得初始化
for(int i=0;i<=2000;i++)
a[i][0]=1;
for(int i=1;i<=2000;i++)
for(int j=1;j<=i;j++)
{
a[i][j]=(a[i-1][j-1]%k+a[i-1][j]%k)%k;//取模很关键,不然直接爆了。
}
到这里总是差不多了吧,下面t次输入,从头到尾找一遍,能被k整除就++。
然而还是太年轻,有白给了TLE(交的时候其实有感觉,t范围太大了)。
然后就卡在这里了,后来经过mhr大佬的帮助,使用前缀和的方法,终于AC了。
我们在打完表之后,就可以记录能被k整除的点了。再用一个二维数组
for(int i=1;i<=2000;i++)
for(int j=1;j<=2000;j++)
{
if(a[i][j]%k==0 && i>=j)
ans[i][j]++;
ans[i][j]+=ans[i][j-1]+ans[i-1][j]-ans[i-1][j-1];
}
这就是这个题的前缀和。
我们可以这样理解ans[i][j],表示i,j左上角所有满足的情况的总和。
所以当我们用 ans[i][j]+=ans[i][j-1]+ans[i-1][j]-ans[i-1][j-1];的时候,如图中有一部分是重合了的,所以要减去这部分。
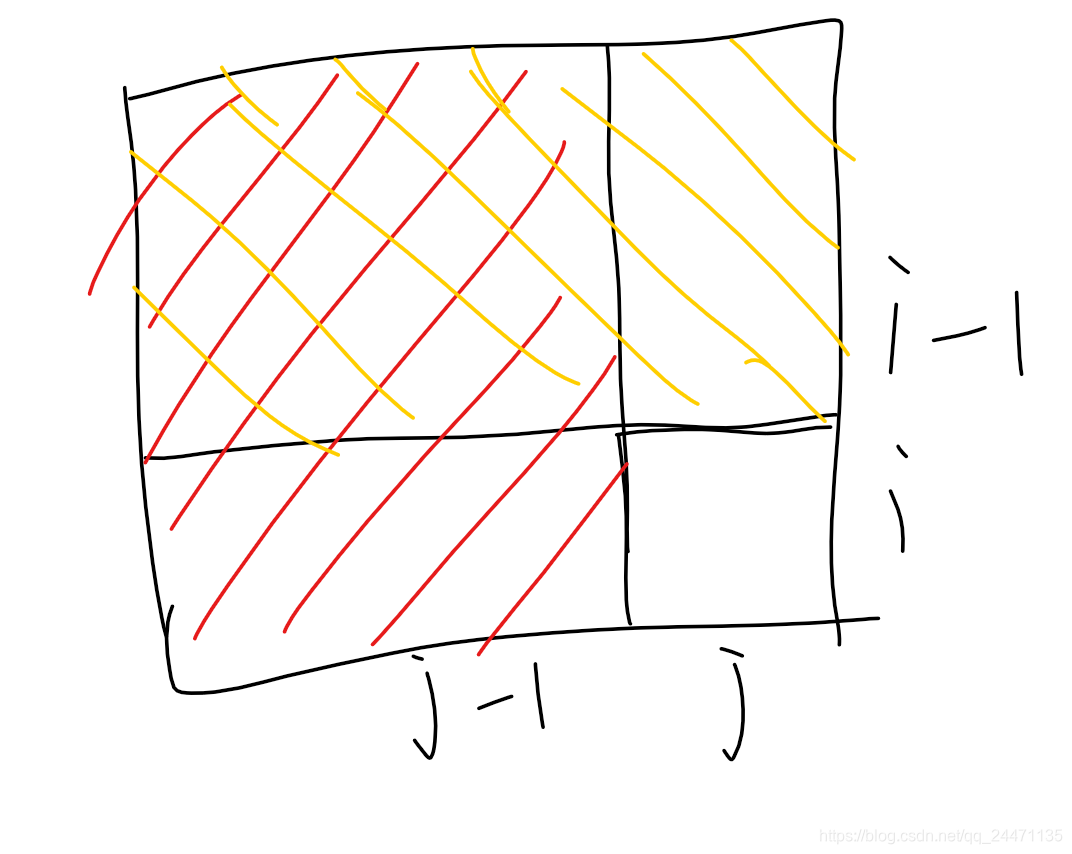
然后这个题就没有什么问题了。
#include<bits/stdc++.h>
using namespace std;
long long a[2001][2001],ans[2001][2001];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n,m,k;
int t;
cin>>t>>k;
for(int i=0;i<=2000;i++)
a[i][0]=1;
for(int i=1;i<=2000;i++)
for(int j=1;j<=i;j++)
{
a[i][j]=(a[i-1][j-1]%k+a[i-1][j]%k)%k;
}
for(int i=1;i<=2000;i++)
for(int j=1;j<=2000;j++)
{
if(a[i][j]%k==0 && i>=j)
ans[i][j]++;
ans[i][j]+=ans[i][j-1]+ans[i-1][j]-ans[i-1][j-1];
}
while (t--) {
cin>>n>>m;
cout<<ans[n][m]<<"\n";
}
return 0;
}
版权声明:
本站所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自
Hao.Jia's Blog!
喜欢就支持一下吧

